Codeforces Round #341 (Div. 2) D. Rat Kwesh and Cheese

問題文はこちら(Problem - D - Codeforces)

まず\( (x^y)^z = (x^z)^y \)であることから\(a_4, a_8, a_{12}\)が候補から外れる。
単純に与えられた式を計算するとオーバーフローしてしまうため、対数をとって比較していく。ただし、\(x < 1\)のとき\( \mathrm{log} x < 0 \)より\( \mathrm{log} \mathrm{log} x\)は(実数上で)存在しない。よってx, y, zの中に1より小さいものが含まれているかどうかで場合分けをする。

(i) x,y,zが全て1より大きい時

\( \{\mathrm{log} \mathrm{log} a_i\}\)の中で最大のものを探す。ただし、最大値を取るものが複数あるときはindexの最も小さいものを選ぶ。

(ii) x, y, zのいずれかが1よりも大きい時

1よりも小さい数が底ならば、今の場合指数は必ず正であるから最終的な値は1よりも小さくなる。逆に1以上の数が底ならば、最終的な値は1以上になる。従って、底が1よりも大きいもののみを(i)と同じように比較すればよい(底が1より小さいものは適当に-INFとかで埋めておく)。

(iii) x,y,zが全て1以下の時

オーバーフローする心配が無いため、\( \mathrm{log} a_i\) の中で最大のものを探せばよい。

コンテストでは\( \mathrm{log} \mathrm{log} x\)が死にうることに気づかず提出してしまった。

#include <bits/stdc++.h>
using namespace std;

#define REP(i,n) for(int i=0;i<(int)(n);i++)
#define ALL(x) (x).begin(), (x).end()

typedef long long ll;
typedef long double ld;

const int INF = 1e9;
const ld EPS = 1e-8;

bool comp(pair<ld,int> p1, pair<ld,int> p2) {
  if(p1.first != p2.first) return p1.first < p2.first;
  return p1.second > p2.second;
}

int main(){
  double x, y, z;
  cin >> x >> y >> z;
  string ans[] = {"x^y^z", "x^z^y", "(x^y)^z", "y^x^z", "y^z^x", "(y^x)^z", "z^x^y", "z^y^x", "(z^x)^y"};
  vector<pair<ld,int>> val(9);

  if(x > 1.0 || y > 1.0 || z > 1.0) {
    if(x > 1.0) {
      val[0] = make_pair(z * log(y) + log(log(x)), 0);
      val[1] = make_pair(y * log(z) + log(log(x)), 1);
      val[2] = make_pair(log(y * z) + log(log(x)) , 2);
    }else{
      val[0] = make_pair(-INF, 0);
      val[1] = make_pair(-INF, 1);
      val[2] = make_pair(-INF, 2);
    }
    if(y > 1.0) {
      val[3] = make_pair(z * log(x) + log(log(y)), 3);
      val[4] = make_pair(x * log(z) + log(log(y)), 4);
      val[5] = make_pair(log(z * x) + log(log(y)) , 5);
    }else{
      val[3] = make_pair(-INF, 3);
      val[4] = make_pair(-INF, 4);
      val[5] = make_pair(-INF, 5);
    }
    if(z > 1.0) {
      val[6] = make_pair(y * log(x) + log(log(z)), 6);
      val[7] = make_pair(x * log(y) + log(log(z)), 7);
      val[8] = make_pair(log(y * x) + log(log(z)) , 8);
    }else{
      val[6] = make_pair(-INF, 6);
      val[7] = make_pair(-INF, 7);
      val[8] = make_pair(-INF, 8);
    }
  }else{
    val[0] = make_pair(pow(y, z) * log(x), 0);
    val[1] = make_pair(pow(z, y) * log(x), 1);
    val[2] = make_pair(y * z * log(x), 2);
    val[3] = make_pair(pow(x, z) * log(y), 3);
    val[4] = make_pair(pow(z, x) * log(y), 4);
    val[5] = make_pair(x * z * log(y), 5);
    val[6] = make_pair(pow(x, y) * log(z), 6);
    val[7] = make_pair(pow(y, x) * log(z), 7);
    val[8] = make_pair(x * y * log(z), 8);
  }

  sort(ALL(val), comp);
  cout << ans[val[8].second] << endl;
  return 0;
}

焼きなまし法でThomson問題の解を探索する

Thomson問題

Thomson問題とは、三次元単位球の表面にN個の電荷の等しい粒子を配置するとき、クーロンポテンシャル\( U = \sum_{i < j} \frac{1}{|\rm{r}_{i} - \rm{r}_{j}|}\)が最小となる配置となるを求める問題です。詳しくはwikiをThomson problem - Wikipedia, the free encyclopedia。N=5のときにて三方両錐形が解になったり、N=8で立方体が解にならないなどいろいろと面白い問題です。

去年の12月頃、そもそもこの問題設定に名前が付いていることをある方から教えていただき、N=5の場合で実際に初期条件を与えて時間発展させることで本当に三方両錐形になるのか実験してみました。

球面上の点電荷が最も安定する配置(thomson problem)のRK4を利用したシミュレーションの進捗 pic.twitter.com/db4FI6wbHe

— 加賀愛 (@the_rain_pelts) December 7, 2014

一応それらしい配置は得られましたが、Uの値が初期値を変える度に大きく変化するのが目につきました。後日、Uの値はNに関して指数関数的に極小点をもつようになり、一般にN粒子のThomson問題はNP困難であることを教えてもらいました。
(参考)http://estamine.net/fc0809/JJFerreira-fisica_computacional.pdf

今回、焼きなまし法で再びこの問題について考えてみました。

焼きなまし法

焼きなまし法自体については以下を主に参照しました。
焼きなまし法 - Wikipedia
shindannin.hatenadiary.com

N個の粒子それぞれの座標を極座標表示したときの偏角の組を状態とします。
近傍状態としては、この2N個の値の中からランダムに一つ選び、平均値が元の値で標準偏差が\( \sqrt{2T}\) (Tは温度)であるような正規分布に従ってランダムに変化させたものを取ります。
また、焼きなましスケジュールは温度が毎回0.9倍になるようにします。

実際のコードは以下の通り

#include <iostream>
#include <vector>
#include <cmath>
#include <climits>
#include <stdexcept>
#include <ctime>
#include <fstream>
using namespace std;

unsigned int randxor(){
  static unsigned int x = 123456789, y = 362436069, z = 521288629, w = 88675123;
  unsigned int t;
  t = (x ^ (x << 11)); x = y; y = z; z = w;
  return (w = (w ^ (w >> 19)) ^ (t ^ (t >> 8)));
}

double uniform(){
  return (double)(randxor()) / UINT_MAX;
}

double rand_normal(double mu, double sigma){
  double z = sqrt(-2.0 * log(uniform())) * sin(2.0 * M_PI * uniform());
  return mu + sigma * z;
}

// if two particles are too close, then throw exception
double eval(vector<double>& state){
  int n = state.size() / 2;
  double energy = 0.0;
  for(int i=0;i<n;++i){
    for(int j=i+1;j<n;++j){
      double dst = sqrt(
        pow(sin(state[2*i]) * cos(state[2*i+1]) - sin(state[2*j]) * cos(state[2*j+1]), 2)
        + pow(sin(state[2*i]) * sin(state[2*i+1]) - sin(state[2*j]) * sin(state[2*j+1]), 2)
        + pow(cos(state[2*i]) - cos(state[2*j]), 2));
      if(dst == 0){
        throw range_error("Diveded by zero.");
      }else{
        energy += 1.0 / dst;
      }
    }
  }
  return energy;
}

double temperature(double r){
  double startTemp = 10.0;
  double alpha = 0.90;
  return startTemp * pow(alpha, r);
}

double probability(double e1, double e2, double temperature){
  if(e1 >= e2){
    return 1.0;
  }else{
    return exp((e1 - e2) / temperature);
  }
}

vector<double> simulated_annealing(int n, int maxIter){
  vector<double> startState(2 * n);
  while(1){
    for(int i=0;i<n;++i){
      startState[2*i] = 2.0 * M_PI * uniform();
      startState[2*i+1] = M_PI * uniform();
    }
    try{
      eval(startState);
      break;
    }catch(range_error& exception){
      continue;
    }
  }
  vector<double> state = startState;
  vector<double> bestState = state;
  double e = eval(state);
  double bestE = e;
  for(int i=0;i<maxIter;++i){
    double temp = temperature((double)i / maxIter);
    
    // change 1 variable to follow normal distribution
    int index = (int)(uniform() * 2 * n);
    double previous = state[index];
    if(index % 2 == 1){
      state[index] = fmod(rand_normal(state[index], sqrt(temp / 2.0)), M_PI);
    }else{
      state[index] = fmod(rand_normal(state[index], sqrt(temp / 2.0)), 2.0 * M_PI);
    }
    
    try{
      double nextE = eval(state);
      if(nextE < bestE){
        bestState = state;
        bestE = nextE;
      }
      if(uniform() <= probability(e, nextE, temp)){
        e = nextE;
      }else{
        state[index] = previous;
      }
    }catch(range_error& exception){
      continue;
    }
  }
  return bestState;
}

int main(){
  ofstream ofs("thomson_step40000.txt");
  for(int n = 1; n <= 50; ++n){
    vector<double> result = simulated_annealing(n, 40000);
    ofs << n << " " << eval(result) << endl;
    cout << n << ": " << eval(result) << endl;
  }
  return 0;
}

結果

N=50までを反復回数20000, 40000のそれぞれで探索しました。最小値は冒頭のwikiに載っています。
真値との相対誤差をプロットしたものが下図

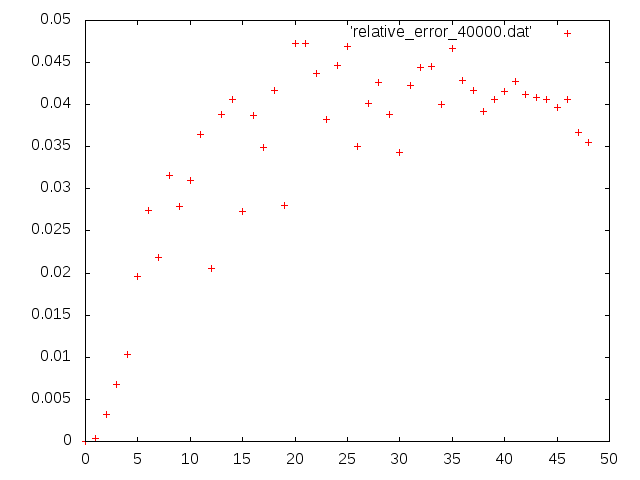
まとめ

お手軽に近似解を出すことができました。焼きなまし法の練習にもよい題材だったと思います。

それと、Thomson問題を焼きなまし法で解く論文はあるようなのですが、有料だったので読めてません。
Generalized simulated annealing algorithm and its application to the Thomson model

SRM 667 Div1 Easy Order Of Operations

どのメモリを使用したかをbitで管理する。
n個の指示を完了するためには、goal := s[0] | s[1] | ... | s[n-1] でbitの立っているメモリを少なくとも一回は使わなければならない。
逆に、goalで立っているbitに対応するメモリを全て実行したならば全ての指示は時間0で実行できる。よって、どのメモリを使用したかだけを情報としてもってbitDPをすればよい。

dp[S] := (Sに対応するメモリを実行するのにかかる時間の総和)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define REP(i, N) for (int i = 0; i < (int)N; i++)

const int INF = 1e9;

class OrderOfOperations {
public:
  vector<string> s;

  int minTime(vector<string> _s) {
    s = _s;
    int n = s.size();
    int m = s[0].size();
    vector<int> dp(1<<m, INF);
    vector<int> a(n,0);
    REP(i,n){
      REP(j,m){
        a[i] *= 2;
        a[i] += s[i][j] - '0';
      }
    }
    int goal = 0;
    REP(i,n) goal = goal | a[i];

    dp[0] = 0;
    REP(S,1<<m){
      REP(i,n){
        int T = S | a[i];
        int cst = 0;
        REP(j,m){
          if(((S >> j) & 1) ^ ((T >> j) & 1)){
            cst++;
          }
        }
        dp[T] = min(dp[T], dp[S] + cst * cst);
      }
    }
    return dp[goal];
  }
};

Richardson補外とか丸め誤差について

『数値計算の常識』(伊理正夫・藤野和建著)を読んでいろいろ試したくなったので、取り敢えず簡単にできるものをやってみる。

定積分\( I = \int_{a}^{b} f(x) dx\)をN等分した台形\(I_N\)で近似するとき、
\( I_{1} = \frac{1}{2}(b - a)(f(a) + f(b)) \)
\( I_{2^{N+1}} = \frac{1}{2} (I_{2^N} + h \sum_{i = 1}^{2^N} f(a + (i - \frac{1}{2})h) ) \), 但し\( h = \frac{b - a}{2^N}\)
で近似値を(逐次的に)出すことができる。

また、f(x)が\(C^{2p}\)級のとき、hに関係しない係数\( d_{2j}\)を用いて
(*)\( I_N - I = \sum_{i=1}^{p} d_{2i} h^{2i} + O(h^{2p+2})\)
と表すことができるらしい(間違っていたらすいません)。

(*)より、上手く数値積分ができているならば、k=1,...,pとして
\( I_{N}^{k} = \frac{ I_{N}^{k - 1} - 4^{-k} I_{N / 2}^{k - 1}}{ 1 - 4^{-k}} \)
但し、\( I_{N}^{0} = I_{N}\)と定めたとき[Richardson補外]、少し計算すると\( I_{N}^{k} - N\)はNが２倍になると\(1 / 4^{k+1}\)倍になること、即ち\( I_{N}^{k} - I_{N/2}^{k}\)はNが２倍になると\(1 / 4^{k+1}\)倍になることが分かる。これより、もしも\( I_{N}^{k}\)の階差を対数目盛でみたときに直線にのっていなければ丸め誤差等の影響で健全な計算が行えていないことが分かる。ちなみに、k=1の場合に得られる近似式はSimpsonの式に一致する。

例として次の(よく例題に出てくる)積分を数値計算で求めることを考える。
\( I = \int_{-1}^{1} \frac{2}{1 + x^2} dx = \pi \)

2^34(=17179869184)等分まで倍精度で求めた。更に、ここから\( I_{N}^{1} \)と \(I_{N}^{2}\)を計算した。

\(I_{N}^{k}\)階差をプロットしたものが下図(順に\(I_{N}, I_{N}^{1}, I_{N}^{2}\)の場合)。

\( N \le 2^{20} \) くらいまでは順調そうだがそれより大きくなると丸め誤差が無視できなくなるようだ。\(I_{2^{20}} = 3.141592653589158068\)であった。

\( N \le 2^9 \) くらいでもう怪しくなっている。\( I_{2^9}^{1} = 3.141592653589792228 \)であった。

ダメダメ。

結果、\(I_{N}^{1}\)を活用することで小数点桁数13桁くらい(3.1415926535897...)まで求めることができた。

実際には直線に乗らない範囲で円周率により近い値を得ているが、本来真値を知っている訳ではないのでそれをより真値に近いものと判断する根拠は乏しい。

[参考]

#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include <cstdio>
using namespace std;

double a = -1.0;
double b = 1.0;

double func(double x){
  return 2.0 / (1.0 + x * x);
}

int main() {
  int M = 34;
  vector<double> integral(M);
  integral[0] = (b - a) * (func(a) + func(b)) / 2.0;
  
  for(int i=1;i<M;++i){
    double middle = 0.0;
    long long N = pow(2, i - 1);
    double h = (b - a) / N;
    
    for(long long i=1;i<=N;i++){
      middle += h * func(a + (i - 0.5) * h);
    }
    
    integral[i] = (integral[i-1] + middle) / 2.0;
  }
  for(int i=0;i<M;i++){
    printf("%lld %.18lf\n", (long long)pow(2, i), integral[i]);
  }
  return 0;
}

N	\(I_{N}\)	\(I_{N}^{1}\)	\( I_{N}^{2}\)
1	2.000000000000000000	0.000000000000000000	0.000000000000000000
2	3.000000000000000000	3.333333333333333037	0.000000000000000000
4	3.100000000000000089	3.133333333333333304	3.555555555555555358
8	3.131176470588235450	3.141568627450980422	3.119999999999999662
16	3.138988494491089298	3.141592502458707248	3.142117647058823682
32	3.140941612041388886	3.141592651224821786	3.141594094125888859
64	3.141429893174974453	3.141592653552836456	3.141592661142562637
128	3.141551963485655019	3.141592653589214912	3.141592653708037641
256	3.141582481063752041	3.141592653589784234	3.141592653591640083
512	3.141590110458282403	3.141592653589792228	3.141592653589822426
1024	3.141592017806918768	3.141592653589797557	3.141592653589792672
2048	3.141592494644073863	3.141592653589791784	3.141592653589798001
4096	3.141592613853361193	3.141592653589790007	3.141592653589791340
8192	3.141592643655684025	3.141592653589791784	3.141592653589790007
16384	3.141592651106267731	3.141592653589795336	3.141592653589791784
32768	3.141592652968914656	3.141592653589796669	3.141592653589795781
65536	3.141592653434578608	3.141592653589800221	3.141592653589796669
131072	3.141592653550970837	3.141592653589768247	3.141592653589800221
262144	3.141592653580073335	3.141592653589774020	3.141592653589766471
524288	3.141592653587365724	3.141592653589796669	3.141592653589774464
1048576	3.141592653589158068	3.141592653589754924	3.141592653589798001
2097152	3.141592653589570183	3.141592653589707851	3.141592653589752260
4194304	3.141592653589582618	3.141592653589587059	3.141592653589704742
8388608	3.141592653589698081	3.141592653589736273	3.141592653589578621
16777216	3.141592653589746931	3.141592653589763362	3.141592653589746487
33554432	3.141592653589535988	3.141592653589465378	3.141592653589765582
67108864	3.141592653589374340	3.141592653589320605	3.141592653589445838
134217728	3.141592653588935136	3.141592653588788586	3.141592653589311279
268435456	3.141592653589452944	3.141592653589625250	3.141592653588753059
536870912	3.141592653589918793	3.141592653590073780	3.141592653589681206
1073741824	3.141592653590653761	3.141592653590898454	3.141592653590103534
2147483648	3.141592653591862572	3.141592653592265805	3.141592653590953521
4294967296	3.141592653595981055	3.141592653597353735	3.141592653592356843
8589934592	3.141592653606938512	3.141592653610590702	3.141592653597693019

AOJ 2333 My friends are small

まず、wを昇順でソートする。
dp[i][j] = #{w[i]以降のみを使って和がjとなる組}
sum[i] = w[i]までの和
とするとき、次の3つの場合を考えれば良い。

(i) w[0]を使わない
(ii) w[0]からw[i]までを使い、w[i+1]を使わない(0 <= i < N-1)
(iii) 全て使う

(i)の場合, (i=1,j) s.t. 0 <= W - j < w[0] について、dp[i][j]をresに加える
(ii)の場合、 (i,j) s.t. 0 <= W - sum[i] - j < w[i+1] について、dp[i][j]をresに加える
(iii)の場合、 W >= sum[N-1] ならばresに1を加える。

#include <bits/stdc++.h>

#define FOR(i,a,b) for(int i=(a);i<(int)(b);++i)
#define REP(i,n) FOR(i,0,n)
#define ALL(x) (x).begin(),(x).end()

using namespace std;

const int INF = 1e9;
const int MOD = 1000000007;

int main() {
  int N,W;
  cin >> N >> W;
  vector<int> w(N),sum(N);
  REP(i,N) cin >> w[i];
  sort(ALL(w));
  sum[0] = w[0];
  REP(i,N-1) sum[i+1] = sum[i] + w[i+1];
  
  vector<vector<int>> dp(N+1, vector<int> (W+1,0));
  dp[N][0] = 1;
  for(int i=N-1;i>=0;i--)REP(j,W+1){
    if(j >= w[i]) dp[i][j] += dp[i+1][j-w[i]];
    dp[i][j] += dp[i+1][j];
    dp[i][j] %= MOD;
  }

  int res = 0;
  if(W >= sum[N-1]) res++;
  REP(j,W+1) if(j > W - w[0]){
    res = (res + dp[1][j]) % MOD;
  }
  REP(i,N-1)REP(j,W+1){
    if(j > W - sum[i+1] && j <= W - sum[i]){
      res = (res + dp[i+2][j]) % MOD;
    }
  }
  cout << res << endl;
  return 0;
}

SRM 664 Div1 Easy Bear Plays

組(X,Y)(X <=Y)を一回操作して(2X,Y-X)にするとき、石の総量S = X + Y は変化しない。よって、少ない方の個数がXのとき、一回の操作後に得られる組の少ない方の個数f(X)は

f(X) = 2X or S - 2X

これをmod S で見ると、f(X) ≡ 2X or -2X であるから、f^K (X) ≡ 2^K * X or -2^K * X

f^K (X) ≡ -2^K * X は個数がS - 2^K * X の場合に対応するから、X = min(A,B)として、min(2^K * X, S - 2^K * X) (mod S) が答えとなる。

#include <bits/stdc++.h>
using namespace std;

#define FOR(i,a,b) for(int i=(a);i<(int)(b);++i)
#define REP(i,n) FOR(i,0,n)

typedef long long ll;

class BearPlays{
public:
  ll modpow(ll K, ll S){
    if(K == 0)return 1;
    if(K % 2) return (2 * modpow(K - 1, S)) % S;
    return (modpow(K/2, S) * modpow(K/2, S)) % S;
  };
  int pileSize(int A, int B, int K){
    ll S = A + B;
    A = min(A, B);
    ll res = (A * modpow(K,S)) % S;
    return min(res, S - res);
  };
};

Codeforces Round #304 (Div. 2) E Soldier and Traveling

sourceとsinkを追加し流量制限にa[i],b[i]を与えることで二部グラフのフローになることは本番中に気づいたが、YESだった場合に経路復元する方法が分からなかった。

考えてみると、逆辺のcapはその辺に流したフローの量であるから、ここから容易に復元することができる。

それと、source=2n, sink=2n+1 みたいに置いておくと、デバッグしやすいことを教えてもらった。

#include <bits/stdc++.h>
using namespace std;

#define REP(i,n) for(int i=0;i<(int)(n);i++)

//Ford-Fulkerson's algorithm
struct edge{int to,cap,rev;};
const int INF=1e9;

void addEdge(vector<vector<edge> > &g,int from,int to,int cap){
    g[from].push_back((edge){to,cap,(int)g[to].size()});
    g[to].push_back((edge){from,0,(int)g[from].size()-1});
}

int dfs(vector<vector<edge> > &g,vector<bool> &used,int v,int t,int f){
    if(v==t) return f;
    used[v]=true;
    for(int i=0;i<(int)g[v].size();i++){
        edge& e=g[v][i];
        if(!used[e.to] && e.cap>0){
            int d=dfs(g,used,e.to,t,min(f,e.cap));
            if(d>0){
                e.cap-=d;
                g[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }
    return 0;
}

int FordFulkerson(vector<vector<edge> > &g,int s,int t){
    int flow=0;
    for(;;){
        vector<bool> used(g.size(),false);
        int f=dfs(g,used,s,t,INF);
        if(f==0) return flow;
        flow+=f;
    }
}
//

int main(){
	int n,m;
    cin >> n >> m;
    vector<int> a(n),b(n);
    REP(i,n) cin >> a[i];
    REP(i,n) cin >> b[i];
    vector<vector<edge> > g(2*n+2);
    int source=2*n;
    int sink=2*n+1;
    REP(i,n) addEdge(g,source,i,a[i]);
    REP(i,n) addEdge(g,n+i,sink,b[i]);
    REP(i,n) addEdge(g,i,n+i,INF);
    REP(i,m){
        int p,q;
        cin >> p >> q;
        addEdge(g,p-1,q-1+n,INF);
        addEdge(g,q-1,p-1+n,INF);
    }
    int sum1=0,sum2=0;
    REP(i,n){
        sum1+=a[i];
        sum2+=b[i];
    }
    int f=FordFulkerson(g,source,sink);
    if(f!=max(sum1,sum2)){
        cout << "NO" << endl;
    }else{
        vector<vector<int> > res(n,vector<int> (n));
        REP(i,n){
            for(auto e : g[i+n]){
                if(e.to<n) res[e.to][i]=e.cap;
            }
        }
        cout << "YES" << endl;
        REP(i,n){
            REP(j,n){
                if(j) cout << " ";
                cout << res[i][j];
            }
            cout << endl;
        }
    }
	return 0;
}