焼きなまし法でThomson問題の解を探索する
Thomson問題
Thomson問題とは、三次元単位球の表面にN個の電荷の等しい粒子を配置するとき、クーロンポテンシャル\( U = \sum_{i < j} \frac{1}{|\rm{r}_{i} - \rm{r}_{j}|}\)が最小となる配置となるを求める問題です。詳しくはwikiをThomson problem - Wikipedia, the free encyclopedia。N=5のときにて三方両錐形が解になったり、N=8で立方体が解にならないなどいろいろと面白い問題です。
去年の12月頃、そもそもこの問題設定に名前が付いていることをある方から教えていただき、N=5の場合で実際に初期条件を与えて時間発展させることで本当に三方両錐形になるのか実験してみました。
球面上の点電荷が最も安定する配置(thomson problem)のRK4を利用したシミュレーションの進捗 pic.twitter.com/db4FI6wbHe
— 加賀愛 (@the_rain_pelts) December 7, 2014一応それらしい配置は得られましたが、Uの値が初期値を変える度に大きく変化するのが目につきました。後日、Uの値はNに関して指数関数的に極小点をもつようになり、一般にN粒子のThomson問題はNP困難であることを教えてもらいました。
(参考)http://estamine.net/fc0809/JJFerreira-fisica_computacional.pdf
今回、焼きなまし法で再びこの問題について考えてみました。
焼きなまし法
焼きなまし法自体については以下を主に参照しました。
焼きなまし法 - Wikipedia
shindannin.hatenadiary.com
N個の粒子それぞれの座標を極座標表示したときの偏角の組を状態とします。
近傍状態としては、この2N個の値の中からランダムに一つ選び、平均値が元の値で標準偏差が\( \sqrt{2T}\) (Tは温度)であるような正規分布に従ってランダムに変化させたものを取ります。
また、焼きなましスケジュールは温度が毎回0.9倍になるようにします。
実際のコードは以下の通り
#include <iostream> #include <vector> #include <cmath> #include <climits> #include <stdexcept> #include <ctime> #include <fstream> using namespace std; unsigned int randxor(){ static unsigned int x = 123456789, y = 362436069, z = 521288629, w = 88675123; unsigned int t; t = (x ^ (x << 11)); x = y; y = z; z = w; return (w = (w ^ (w >> 19)) ^ (t ^ (t >> 8))); } double uniform(){ return (double)(randxor()) / UINT_MAX; } double rand_normal(double mu, double sigma){ double z = sqrt(-2.0 * log(uniform())) * sin(2.0 * M_PI * uniform()); return mu + sigma * z; } // if two particles are too close, then throw exception double eval(vector<double>& state){ int n = state.size() / 2; double energy = 0.0; for(int i=0;i<n;++i){ for(int j=i+1;j<n;++j){ double dst = sqrt( pow(sin(state[2*i]) * cos(state[2*i+1]) - sin(state[2*j]) * cos(state[2*j+1]), 2) + pow(sin(state[2*i]) * sin(state[2*i+1]) - sin(state[2*j]) * sin(state[2*j+1]), 2) + pow(cos(state[2*i]) - cos(state[2*j]), 2)); if(dst == 0){ throw range_error("Diveded by zero."); }else{ energy += 1.0 / dst; } } } return energy; } double temperature(double r){ double startTemp = 10.0; double alpha = 0.90; return startTemp * pow(alpha, r); } double probability(double e1, double e2, double temperature){ if(e1 >= e2){ return 1.0; }else{ return exp((e1 - e2) / temperature); } } vector<double> simulated_annealing(int n, int maxIter){ vector<double> startState(2 * n); while(1){ for(int i=0;i<n;++i){ startState[2*i] = 2.0 * M_PI * uniform(); startState[2*i+1] = M_PI * uniform(); } try{ eval(startState); break; }catch(range_error& exception){ continue; } } vector<double> state = startState; vector<double> bestState = state; double e = eval(state); double bestE = e; for(int i=0;i<maxIter;++i){ double temp = temperature((double)i / maxIter); // change 1 variable to follow normal distribution int index = (int)(uniform() * 2 * n); double previous = state[index]; if(index % 2 == 1){ state[index] = fmod(rand_normal(state[index], sqrt(temp / 2.0)), M_PI); }else{ state[index] = fmod(rand_normal(state[index], sqrt(temp / 2.0)), 2.0 * M_PI); } try{ double nextE = eval(state); if(nextE < bestE){ bestState = state; bestE = nextE; } if(uniform() <= probability(e, nextE, temp)){ e = nextE; }else{ state[index] = previous; } }catch(range_error& exception){ continue; } } return bestState; } int main(){ ofstream ofs("thomson_step40000.txt"); for(int n = 1; n <= 50; ++n){ vector<double> result = simulated_annealing(n, 40000); ofs << n << " " << eval(result) << endl; cout << n << ": " << eval(result) << endl; } return 0; }
結果
N=50までを反復回数20000, 40000のそれぞれで探索しました。最小値は冒頭のwikiに載っています。
真値との相対誤差をプロットしたものが下図

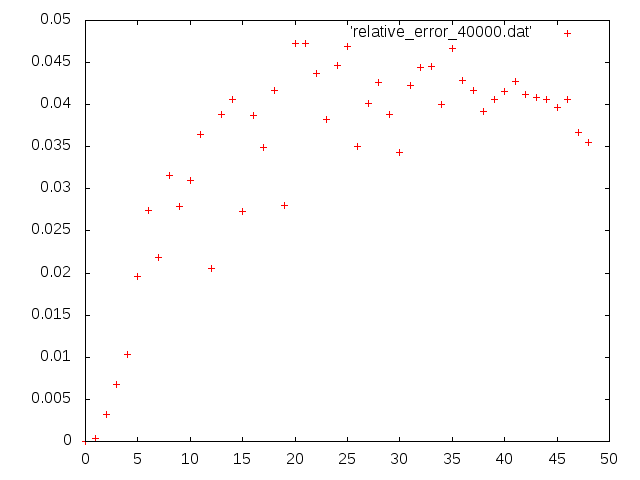
まとめ
お手軽に近似解を出すことができました。焼きなまし法の練習にもよい題材だったと思います。
それと、Thomson問題を焼きなまし法で解く論文はあるようなのですが、有料だったので読めてません。
Generalized simulated annealing algorithm and its application to the Thomson model